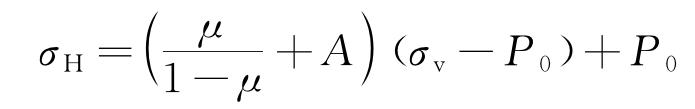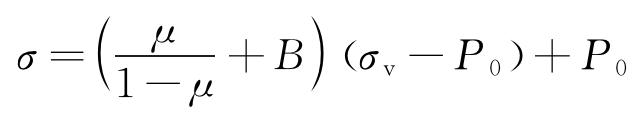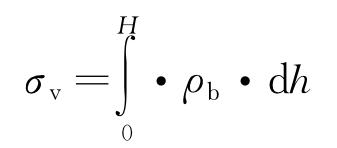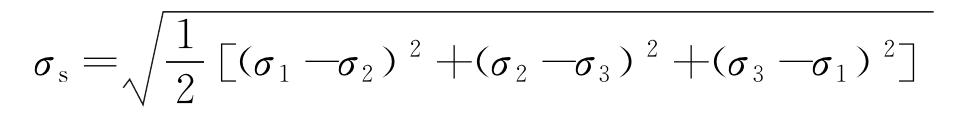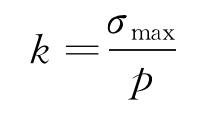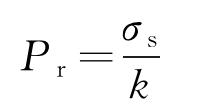腐蚀缺陷形状对套管损伤的影响

2025-02-20 15:16:17 作者：幸雪松来源：腐蚀与防护分享至：

随着深井、超深井油气资源的开采,套管面临的腐蚀问题日益严重[1-2]。在复杂的工作环境中,套管既有来自地层流体压力和地应力的机械挤压作用,也有来自含腐蚀介质油气对套管的化学作用[3-6]。套管腐蚀会直接影响井筒的完整性和油田企业的安全生产[7-8]。因此,对腐蚀套管进行应力和剩余强度分析是尤为重要的。

在套管腐蚀研究领域,国内外学者主要以电化学、弹塑性力学、断裂力学等为理论基础[9],研究套管的腐蚀机理、剩余强度以及腐蚀速率等,并推出了一系列评估规范和方法。祝效华等[10]通过对不同形貌腐蚀缺陷进行规则化处理,研究了腐蚀缺陷类型对套管抗挤压强度的影响。ZHANG等[11]建立了复合模态下套管磨损形态和剩余强度的预测模型,揭示了各种因素对套管强度的影响。NARHI等[12]采用热-机械井模拟器和有限元模型分析了油井套管的严重腐蚀问题,评估了油井的结构完整性。MOHD等[13]利用有限元模型,分析了内压和弯矩共同作用对套管剩余强度的影响规律。车争安等[14]通过建立腐蚀孔应力集中系数的数学模型和剩余强度计算公式,研究了应力集中对套管强度的影响。NABIPOUR等[15]通过有限元方法模拟了井下环境,研究了内压、水平应力差和套管偏心对套管稳定性的影响。张智等[16]通过建立腐蚀套管强度计算模型,研究了温度、内压、腐蚀深度、直径因素对套管等效应力和剩余强度的影响规律。上述研究表明,应力与腐蚀的协同作用会加剧套管的腐蚀,造成套管材料提前失效。

针对上述问题,笔者以焦页4HF井中139.7 mm直径、N80钢级的套管为例,在现有理论研究基础上,针对套管腐蚀后腐蚀缺陷形状复杂多变的特点,选择三类常见腐蚀缺陷形状（凹槽形、圆球形和半圆柱形）[17],分别建立“套管-水泥环-地层”三维模型。采用有限元方法,研究了腐蚀缺陷几何形状和腐蚀影响因素对套管腐蚀区域应力分布情况、Von Mises等效应力和剩余强度的影响,从而得出对套管性能影响最大的腐蚀缺陷形状,在此基础上,同时考虑了温度、内外压差等因素,对含圆球形腐蚀缺陷组合体进行稳态热-结构耦合分析。以期为含腐蚀缺陷套管的安全评价和井筒完整性评估提供技术支持。

1. 不同腐蚀缺陷形状套管的有限元模型

钻井过程中,套管的力学性能受温度、压力、地应力、腐蚀性介质等因素的影响。考虑到套管各方面存在性能差异,在采用有限元软件进行模拟时,不能完全模拟油套管的受力情况。为了便于建立三维模型,对“套管-水泥环-地层”模型进行如下基本假设[18-19]：

（1）系统所有材料都是均匀的、连续的,且都为弹性体；

（2）套管、水泥环、地层三者之间的接触部位胶结良好、无滑动,水泥环和井壁围岩均为均匀且各向同性体；

（3）套管、水泥环、地层为同心圆柱；

（4）水泥环中没有初始应力；

（5）系统受力是平面应变。

1.1 模型建立

根据岩石力学和弹塑性力学理论,以套管-水泥-地层系统为研究对象,具体参数如表1所示。考虑实际油气井状况,为减少有限元模型的运算量,选取部分长度进行研究,取地层的外径为1 200 mm,水泥环的外径为215.9 mm,根据圣维南原理[20],系统整体长度取4 000 mm,以更好地消除边界效应的影响。

表 1 “套管-水泥环-地层”系统的参数

Table 1. Parameters of “casing-cement sheath-stratum” system

参数	弹性模量/MPa	泊松比	内径/mm	外径/mm	热膨胀系数/（×10-6 ℃-1）	导热系数/（W·m-1·℃-1）
套管	210 000	0.30	118.62	139.7	18.2	50.50
水泥环	10 000	0.17	139.70	215.9	10.0	0.95
地层	22 000	0.23	215.90	1 200.0	10.0	1.92

1.2 网格划分

根据建立的“套管-水泥环-地层”三维有限元模型,采用由外向内逐级细化分段的方法扫描划分网格,对套管局部腐蚀区域采用网格加密处理,见图1。

图 1 含不同形状腐蚀缺陷套管的有限元模型及网格划分

Figure 1. Finite element model and mesh division of casing with corrosion defects of groove shape (a), spherical shape (b) and semi-cylindrical shape (c)

1.3 载荷的边界条件

垂直井眼周围地层岩石受力主要包括上覆岩层压力、岩石内孔隙流体的压力及水平地应力。油气井生产时,套管受力情况复杂,不仅受到内部流体压力、轴向载荷、摩擦载荷、屈曲载荷,还受到来自地层的非均匀地层应力等。此外,整个系统还受到温度载荷的作用[21],如图2所示。图2中,σv为上覆岩层压力；σH为水平最大主应力；σ为水平最小主应力；P0为岩石孔隙流体压力。

图 2 井眼周围岩石受力示意

Figure 2. Schematic of rock force around the wellbore

上覆岩层压力σv来源于上部岩石的重力,它和岩石内孔隙流体压力的差（σv-P0）为有效上覆岩层压力,水平地应力σH及σ来自垂直方向上的有效上覆岩层压力和地质构造力。地层水平地应力可以描述为[22]：

(1)

(2)

(3)

式中：μ为地层弹性模量；A,B为构造应力系数；ρb为地层密度。

本模型忽略和简化了影响较小的载荷,套管仅受内压、外压和温度作用。为了简化不均匀的地层压力,将最大和最小水平应力简化为均匀围压,附加在地层周围,模型简化受力分析如图3所示。“套管-水泥-地层”采用底端固定约束。

图 3 模型受力分析示意

Figure 3. Schematic of model force analysis

1.4 套管腐蚀后剩余强度计算准则

当材料局部腐蚀区域任意一点的等效应力达到材料的屈服强度时,即发生失效。依据第四强度理论,将等效应力屈服准则作为套管失效的判定准则,Von Mises应力可表述为

(4)

式中：σs为屈服应力；σ1、σ2、σ3分别为x、y、z方向上的主应力。

套管在内外压的作用下,在弹性和小变形范围内,其最大等效应力σmax和所受内压或外压之比是一个常数k。

(5)

式中：σmax为套管最大Von Mises应力；p为套管所受内压或外压。

当压力作用在套管上使其应力达到屈服强度时,将会产生塑性变形,套管极易发生变形导致损坏,根据拉梅公式,推导出套管的剩余强度公式。

(6)

式中：Pr为套管剩余强度,MPa;σs为套管的屈服强度,MPa。

1.5 仿真模型验证

为了验证所建模型的合理性和可行性,计算了有限元数值解和API标准抗挤强度（API Bul5C2）的相对误差,并与相关文献中的数据结果进行对比[10]。分别选取相同尺寸不同钢级的套管作为研究对象,设置与文献中相同的初始条件,求解不同钢级套管的抗挤强度,得到不同钢级套管的相对误差,并与文献结果进行对比,如图4所示。本模型相对误差为1.3%~6.6%,比文献结果误差更小,符合工程计算要求。

图 4 模拟结果与文献结果对比

Figure 4. Comparison of simulation results and literature results

2. 实例分析

选取焦页4HF井地下3 500 m处的“套管-水泥环-地层”组合体为研究对象进行分析。研究凹槽形腐蚀坑、圆球形腐蚀坑、圆柱形腐蚀坑三种腐蚀缺陷对套管应力和剩余强度的影响。套管材料为N80钢级,尺寸为139.7 mm×10.54 mm,弹性模量210 GPa,泊松比0.3,屈服强度552 MPa,抗拉强度689 MPa。

2.1 凹槽形局部腐蚀坑对套管损伤分析

腐蚀对套管强度的影响主要是由于腐蚀区域边缘处产生了应力集中,改变了套管在腐蚀区域边缘处的应力分布和整体强度。影响套管强度的主要因素有腐蚀长度、腐蚀宽度和腐蚀深度。

2.1.1 腐蚀宽度的影响

由图5可见：随着腐蚀凹槽宽度的增加,套管腐蚀区域中间部位应力逐渐减小,腐蚀边缘应力逐渐增大,最大应力发生在腐蚀区域与套管内壁相交处,且腐蚀区域应力呈对称状分布。

图 5 不同腐蚀凹槽宽度条件下的套管应力分布云图

Figure 5. Cloud maps of stress distribution in casing under different corrosion groove width conditions

由图6可见：随腐蚀凹槽宽度的增加,套管的等效应力呈先急剧增大后减小再趋于平缓的趋势,套管剩余强度呈先急剧减小后增大再趋于平缓的趋势。在腐蚀宽度为5 mm附近出现应力最大值,是因为当腐蚀凹槽宽度较小时,腐蚀区域应力集中现象明显,套管剩余强度急剧降低。腐蚀凹槽宽度增大到10 mm后,套管等效应力和剩余强度变化较小。当腐蚀凹槽深度为4 mm时,套管极易发生失效；当腐蚀凹槽深度超过4 mm后,套管等效应力大于屈服强度,根据失效判定准则,此时套管已失效。

图 6 不同腐蚀凹槽宽度条件下套管的等效应力和剩余强度

Figure 6. Equivalent stress (a) and residual strength (b) of casing under different corrosion groove width conditions

2.1.2 腐蚀长度的影响

由图7可见：随着腐蚀凹槽长度的增加,腐蚀区域中间的应力逐渐增大,沿着长度增加方向,边缘处应力也逐渐增大,且腐蚀区域应力呈对称分布。

图 7 不同腐蚀凹槽长度条件下的套管应力分布云图

Figure 7. Cloud maps of stress distribution in casing under different corrosion groove length conditions

由图8可见：随着腐蚀凹槽长度的增加,套管的等效应力先急剧增加后趋于平缓,剩余强度先急剧减小后趋于平缓。腐蚀凹槽长度增加,腐蚀面积增大,因此套管等效应力增大、剩余强度减小。当腐蚀深度为6 mm、长度为50 mm时,套管已达到屈服强度,极易发生失效；当腐蚀深度低于6 mm、长度小于100 mm时,套管处于安全服役状态。

图 8 不同腐蚀凹槽长度条件下,套管的等效应力和剩余强度

Figure 8. Equivalent stress (a) and residual strength (b) of casing under different corrosion groove length conditions

对比图6和图8可知,深度的变化对套管性能的影响极大,随着腐蚀深度的增加,套管等效应力和剩余强度的变化幅度大于腐蚀宽度和长度变化引起的应力和剩余强度的变化幅度。腐蚀腐蚀凹槽长度的增加会使应力缓慢增大,而凹槽宽度的增加,则对应力变化影响较小,说明长度因素对套管性能的影响大于宽度因素。综上所述,套管腐蚀凹槽深度因素对套管最大等效应力和套管剩余强度的影响最大,长度因素次之,宽度因素最小。

2.2 圆球形局部腐蚀坑对套管损伤分析

图9中腐蚀凹陷深度比定义为腐蚀深度与套管壁厚之间的比值。由图9可见：随着腐蚀凹陷深度比增加,腐蚀区域底部应力逐渐减小,环向应力逐渐增大,最大应力出现在腐蚀区域与套管内壁相交的位置。

图 9 圆球形腐蚀坑条件下,不同腐蚀凹陷深度比的套管应力分布云图

Figure 9. Stress distribution cloud maps of casing with different corrosion depression depth ratios under spherical corrosion pit condition

分析不同圆球形腐蚀半径和不同腐蚀凹陷深度比对套管等效应力和剩余强度的影响规律,如图10所示。

图 10 圆球形腐蚀坑条件下,腐蚀半径和凹陷深度比对套管等效应力和剩余强度的影响

Figure 10. The influence of corrosion radius (a) and depression depth ratio (b) on equivalent stress and residual strength of casing under spherical corrosion pit condition

由图10可见：套管等效应力随腐蚀凹陷深度比增加大致呈三次函数上升趋势,套管剩余强度随腐蚀凹陷深度比增加呈下降趋势,当腐蚀凹陷深度比小于30%时,等效应力和剩余强度曲线斜率随着凹陷深度比的增大逐渐减小,这是因为随着套管腐蚀凹陷深度逐渐增大,腐蚀区域应力集中现象减弱,不同腐蚀半径导致的套管等效应力和剩余强度变化较小。当腐蚀凹陷深度比大于30%时,随着腐蚀凹陷深度比增大,等效应力和剩余强度曲线斜率出现明显增大。此外,腐蚀坑半径越大,等效应力越大,其主要原因是随着腐蚀凹陷深度和腐蚀坑半径增大,套管腐蚀面积增大,套管整体强度降低。当腐蚀凹陷深度比大于70%后,套管腐蚀后应力大于其屈服强度,套管易发生失效。

2.3 半圆柱形局部腐蚀坑对套管损伤分析

由图11可见：随着腐蚀长度的增加,等效应力逐渐增大,且最大应力发生在腐蚀区域的底部。

图 11 半圆柱形腐蚀坑条件下,不同腐蚀长度套管的应力分布云图

Figure 11. Stress distribution cloud maps of casing with different corrosion lengths under semi cylindrical corrosion pit condition

由图12可见：随着腐蚀长度的增加,套管等效应力整体大致呈对数函数增大的趋势,套管剩余强度大致呈对数函数递减趋势,当腐蚀长度为20 mm时,应力值达到了套管屈服应力极限,此时套管剩余强度为28 MPa。当腐蚀长度小于20 mm时,随着腐蚀长度的增加,腐蚀半径越小,套管等效应力越大,这主要是因为腐蚀半径越小,套管应力集中现象越明显,应力变化越大。当腐蚀长度大于20 mm后,随着长度的增加,半径越大,应力越大,此时应力增大的主要受腐蚀面积的影响。

图 12 半圆柱形腐蚀坑条件下,腐蚀半径和长度对套管等效应力和剩余强度的影响

Figure 12. The influence of corrosion radius (a) and length (b) on the equivalent stress and residual strength of casing under semi cylindrical corrosion pit condition

3. 圆球形腐蚀坑对套管损伤分析

通过对含三种几何形状腐蚀缺陷的套管进行有限元分析,比较得出圆球形腐蚀坑对套管性能影响最大,为了进一步分析腐蚀对套管性能的影响,对圆球形腐蚀坑进行深入研究,对含圆球形腐蚀坑“套管-水泥环-地层”组合体进行稳态热-应力耦合分析,在上述研究基础上考虑温度、内外压差等因素对套管的影响。

前文研究表明,套管腐蚀后应力最大部位出现在腐蚀区域。为深入研究腐蚀区域应力分布情况以及腐蚀对套管的影响,对圆球形腐蚀坑区域以径深2 mm分别选取三个平面,且第一平面为腐蚀坑与套管内壁相交平面,第二平面距第一平面2 mm,第三平面距第二平面2 mm,三个平面的应力分布如图13所示。可以看出,三个平面内应力均呈对称分布,第一平面、第二平面、第三平面内应力依次减小,可见,径深越大,应力越小。

图 13 圆球形腐蚀坑条件下,不同平面的内应力分布图

Figure 13. Distribution diagram of internal stress in different planes under the condition of spherical corrosion pits

在不同压差作用下套管第一平面应力分布情况如图14（a）所示,与第一平面垂直平面即与套管圆周方向平面的平面应力分布如图14（b）所示,可以看出,该平面内腐蚀区域底部应力最大,分析可知腐蚀后套管应力较大位置出现在沿轴向方向第一平面两侧、腐蚀区域底部,可以进一步判断套管将沿着轴向以及腐蚀深度方向产生腐蚀延伸。

图 14 应力分布随距离、内外压差变化

Figure 14. Variation of stress distribution with distance and pressure difference between inside and outside:（a) stress distribution diagram of the first plane of the casing;（b) phane stress distribation diagram of circuferential of the casing

由图15可知：随着腐蚀凹陷深度比和套管压差的增大,套管等效应力先增大后减小,再逐渐增大,当腐蚀凹陷深度比为50%时出现应力突增；套管受压差的影响较大,压差越大,应力越大,变形量越大。