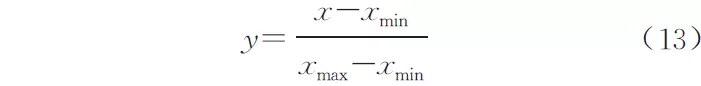基于深度学习的海底管道外腐蚀剩余强度评估

2021-08-24 16:03:31 作者：谢鹏来源：油气储运科技界分享至：

海底管道作为海上油气开发必须依赖的重要基础设施，是海洋油气资源开发的生命线[1]。在油气田内部，海底管道将海上油气田的钻井系统、生产系统及海底管汇连成一体，使钻井、采油及输运系统相互关联、相互协调。在油气外输作业中，海底管道跨越复杂海床，与岸基终端设备相连，快速、高效地完成油气的运输过程。在服役过程中，海底管道受水压、CO2、温度、盐度及海洋生物等海洋复杂环境的影响，容易发生腐蚀失效。腐蚀是造成海底管道失效的主要因素，不仅削弱管道的剩余强度，甚至影响管道的安全运行。在海底管道的所有失效类型中，腐蚀引起的管道失效占比高达35％[2-3]。为了保证海底管道的安全运行，需要对管道的腐蚀情况进行定期检查，并预测管道的腐蚀剩余强度，进一步确定含腐蚀缺陷管道的后续承载能力及服役状态。

管道的腐蚀剩余强度评估，是研究含腐蚀缺陷的管道在某一工作压力下的受力状态，计算管道的最大等效应力，并判断管道是否会发生强度失效，为管道的运行和维护提供建议。在评估标准方面，1999 年英国燃气公司（BG）和挪威船级社（DNV）针对含缺陷管道剩余强度开展了研究，提出了DNVOS-F101-2000《挪威船级社海底管线系统规范》，其中规定了分项安全系数法和许用应力法；2009 年美国天然气协会Kiefner 等优化了早年提出的较为保守的ASME B31G-1984《美国机械工程师协会标准-已腐蚀管线剩余强度评估手册》计算标准，推出了ASMEB31G-2009《美国机械标准中文版标准目录-已腐蚀管线剩余强度评估手册》，成为目前国际上应用最广泛的标准规范。在数值仿真方面，2000 年，美国Battelle实验室基于有限元分析方法，评估了管道的剩余强度，提出了PCORRC[4]（Pipeline Corrosion Criterion）方法；2008 年，帅健等[5]通过数值分析方法拟合得到腐蚀管道失效压力预测公式，并进行了试验验证；2016 年，艾志久等[6]基于数值仿真方法对含外腐蚀缺陷管道剩余强度及剩余寿命进行了研究；同年，于桂杰等[7]基于有限元方法研究了海底管道腐蚀剩余强度的评估方法；2018 年，黄宇立等[8]针对纯内压作用下单缺陷腐蚀海底管道的安全性进行了数值模拟；2018 年，冯欣鑫等[9]针对双腐蚀缺陷海底管道临界失效压力进行了数值仿真分析；2019 年，王战辉等[10]对含双点腐蚀的管道剩余强度和剩余寿命进行了分析。在试验研究方面，1998 年，陈建民等[11]开展了内压爆破试验研究，通过对表面有特定缺陷的不同材质、不同管径试验管材进行水压爆破试验，并将爆破试验结果与美国标准中的理论计算结果进行对比，验证了美国管道法规在中国的适用性；2000 年，Freire 等[12]进行了X60 轴向长腐蚀管道的爆破试验；2006 年，帅健等[13]收集了63 组腐蚀缺陷管道全尺寸爆破试验结果，并基于全尺寸爆破试验数据，分别使用ASME B31G-1984、DNVRP-F101-1999《管道剩余强度评价标准》及PCORRC评定方法计算管道失效压力，研究了以上规范的适用性；2017 年，张少轩[14]开展了基于深度学习的缺陷深度反演研究，在预测管道缺陷深度的形态尺度上验证了深度学习的精度；2020 年，刘明[15]提出对于缺陷金属，基于深度学习构筑的模型可在极短时间内模拟出表面缺陷的具体情况；同年，滕帅[16]基于深度学习开展结构损伤识别方法研究，证明了卷积神经网络在识别缺陷损伤与计算方面有明显的优越性。

目前，已有研究在海底管道腐蚀残余寿命预测方面存在诸多局限性，如概率统计学在缺乏数据的情况下，预测精度往往不满足要求。人工神经网络方法是当前应用较为广泛的一种深度学习方法，其结构较为简单。国际上最新的腐蚀剩余寿命预测思路是利用可靠性函数分析方法将高分辨率的管道漏磁检测技术与适用性评价技术相结合，但技术较为复杂。这些方法在解决腐蚀残余寿命预测中的非线性问题时，其准确度较差。在此，首先使用数值仿真方法，对含外腐蚀缺陷海底管道进行非线性有限元分析，研究含有不同尺寸外腐蚀缺陷海底管道的剩余强度；然后，基于深度学习理论建立腐蚀缺陷与管道等效应力之间的非线性预测模型；最后，将二者结果进行对比，验证基于深度学习模型预测含外腐蚀缺陷海底管道剩余强度的可行性，为解决腐蚀残余寿命预测提供有效参考。

1　非线性有限元分析

基于ABAQUS 软件建立含外腐蚀缺陷海底管道的非线性有限元分析模型，计算管道在内压荷载作用下的最大等效应力和腐蚀剩余强度，评估外腐蚀缺陷的深度、长度、宽度对海底管道剩余强度的影响。

1.1 有限元模型

建立含外表面腐蚀缺陷的海底管道有限元分析模型（图1）。在模型中，管道长3 000 mm，外径762 mm，壁厚17.5 mm，外表面含有局部腐蚀缺陷。由于模型的对称性，为节省计算资源，采用管道的1/4 模型进行研究。模型选用八节点六面体缩减积分实体单元C3D8R 模拟管道，并在划分网格时对局部外腐蚀缺陷处进行网格加密以避免应力集中，模型径向网格层数约为5 层，单元总数约为40 000 个，能够保证计算精度[17]。

图1　含外表面腐蚀缺陷的海底管道有限元分析模型图

为考虑管道材料（表1）的非线性特征，采用Romberg-Osgood 方程建立管道材料的本构关系，其表达式为：

式中：E 为弹性模量，MPa；ε 为应变；σ 为应力，MPa；σs 为屈服应力，MPa；A 为硬化系数，A=1.29；B 为幂硬化指数，B =25.58。

表1　管道材料属性参数

式（1）能够反映该种材料的管道在屈服后的硬化性能[18]，根据此方程可得出X65钢管的应力应变关系。

1.2 载荷与边界条件

设置边界条件（图2）：管道两端横截面轴向位移为0，忽略管道在海底的横向和轴向位移；轴向剖面为对称全约束，含缺陷处管道横截面为对称约束。在管道内壁施加均匀内压，根据NG-18-1969《美国燃气协会标准》、ASME B31G-2009、DNV-RP-F101-1999 以及PCORRC 评定方法中的理论公式计算不同腐蚀缺陷尺寸下管道的失效内压pe，因此，在管道内壁施加的内压变化范围为pe±2 MPa。首先，在管道内壁施加pe-2 MPa 的压力，并以1 MPa 的步长逐步递增；当管道内压增至p 时管道发生失效，则缩小管道内压步长重新进行试算。重新在管道内壁施加p-1 MPa 内压，并以步长为0.1 MPa 逐步增加，在压力区间（p-1，p ）内确定使含腐蚀缺陷管道达到极限承载能力的失效内压，即为管道的腐蚀剩余强度。

图2　管道有限元分析模型边界条件设置图

1.3 模拟结果

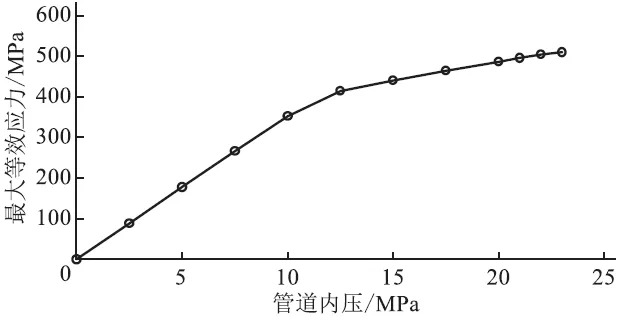
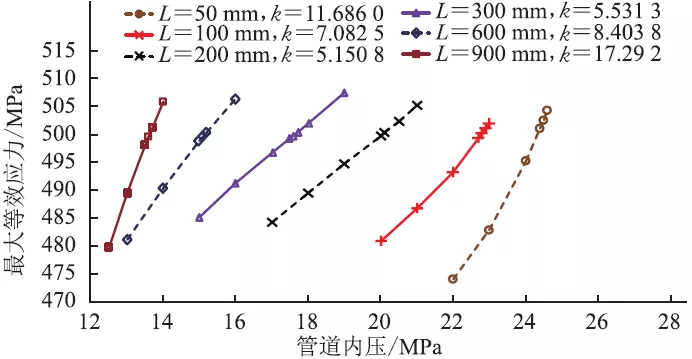
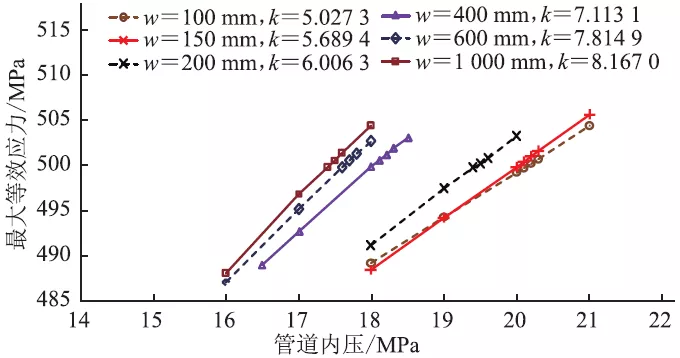
为研究外腐蚀缺陷的深度d 、长度L 、宽度w 对管道腐蚀剩余强度的影响，基于有限元分析方法，建立了114 组含不同腐蚀缺陷尺寸的海底管道分析模型，计算在内压荷载作用下的管道最大等效应力（图3，其中k 为连线的斜率）。当管道内压荷载较小时，管道处于弹性范围内，管道的最大等效应力随内压荷载的增大呈线性增长；当最大等效应力超过屈服强度后，管道发生塑性变形，最大等效应力随管道内压的增大呈非线性增长（图3a），但增长幅度逐渐变小，管道最大等效应力与腐蚀缺陷的几何尺寸密切相关，其值随腐蚀缺陷的深度、长度及宽度的增加而逐渐变大（图3b~图3d）。

（a）d =7.0 mm，L =200 mm，w=50 mm

（b）L =200 mm，w=50 mm

（c）d =8.75 mm，w=50 mm

（d）d =8.8 mm，L =200 mm

图3　含腐蚀缺陷管道最大等效应力随管道内压的变化曲线

2　深度学习预测模型

2.1 基本原理

深度学习作为机器学习的分支，受到广泛关注，可以高效解决以往对人工智能极具挑战性的任务。在深度学习中，最具代表性的模型是深度神经网络（Deep Neural Network，DNN）。神经网络类似大脑的工作机制，以节点模拟大脑中的神经元，构成一个复杂的网络。在神经网络中，信息以权重和偏差的形式存储。外界输入信号在到达节点前，首先与权重相乘，再进入神经网络进行处理，其加权和计算过程如下：

式中：vi （1）为隐藏层节点的加权和；ωij （1）为第2 层输出节点i 与输入节点j 之间的权重；bi （1）为第2 层第i 个单元的偏置项；yi （1）为隐藏层节点i 的输出；φ（v ）为隐藏层和输出层的激活函数[19]；v 为输入信号的加权和；y 为通过激活函数的加权和的输出。

按照隐藏层的数目不同，神经网络可分为单层神经网络和多层神经网络，其中只有一个隐藏层的神经网络称为单层神经网络，具有多个隐藏层的神经网络称为深度神经网络。

2.2 BP 深度神经网络模型建立

在单层神经网络中，第1 层是输入层L1（Input Layer），第2 层是隐藏层L2（Hidden Layer），第3 层是输出层L3（Output Layer）。深度神经网络的隐藏层数目较多，更适于处理非线性问题。每一个隐藏层都可以在前一层提取到的信息上进行组合。因此，隐藏层数目越多，深层神经网络模型中需要计算的参数也越多，能够学习和处理的问题也更复杂。在神经网络中，误差的传递通常使用误差反向传播算法（Error Back Propagation Training，BP），系统解决了多层神经网络隐藏层连接权学习问题，并在数学上给出了完整推导，使用这种算法进行误差校正的多层前馈网络称为BP神经网络。建立深度神经网络模型的具体步骤如下：

（1）确定输入输出数据，将影响管道失效内压的因素作为输入层数据，即输入层神经元数为4；将管道的等效应力作为输出层数据，即输出层神经元数为1。

（2）合理选择隐藏层个数，在此训练一个含有4 层隐藏层的深度神经网络，根据经验公式式（12）选择隐藏层神经元个数[20]。通过测试发现12 个神经元效果最好，因此选取12 为建立的神经网络中隐藏层的神经元数，构建深度神经网络结构（图4）。

式中：a ' 为隐藏层神经元数；a 为输入层的节点个数；b 为输出层的节点个数；n 为常数。

图4　腐蚀管道剩余强度预测深度神经网络结构示意图

（3）输入层与隐藏层之间的激活函数选tansig 函数，隐藏层与输出层之间的连接函数选线性函数。

（4）采用随机梯度下降法、动量法及学习率自适应调整方法来训练神经网络[21]。在输入层中，以腐蚀缺陷的长度、宽度、深度以及管道的工作内压作为输入层变量，以管道的最大等效应力作为输出层变量。

2.3 深度神经网络模型训练

选取163 组有限元计算结果作为样本数据进行深度学习模型训练，其中70％的数据用于训练神经网络，作为训练集；30％的数据作为测试样本预测不同腐蚀程度下的最大等效应力，作为测试集。为保证模型的可靠性和真实性，在模型训练中，所有的样本数据在训练与预测过程中是随机分布的。为了提高神经网络模型的训练效率，防止神经网络训练时部分神经元达到过饱和状态，对163 组有限元计算数据进行归一化处理，归一化公式[22]为：

式中：y 为归一化后的值；x 为归一化前的值；xmax 为样本数据中的最大值；xmin 为样本数据中的最小值。

基于深度学习模型训练神经网络时，模型参数设置如下：神经网络误差为10-6，网络学习率η =0.07，神经网络训练次数为10 000 次，附加动量因子为0.95，最小性能梯度为10-6。以训练集的114 组有限元分析结果作为数据集，对含腐蚀缺陷海底管道剩余强度评估模型进行训练，得到训练结果回归曲线（图5，其中R2表示相关系数）。结果显示：训练回归系数为0.996 07，均方误差为0.000 54，均在误差范围之内，验证了神经网络模型训练结果的可靠性。

图5　BP 神经网络模型训练回归曲线图

3　结果对比

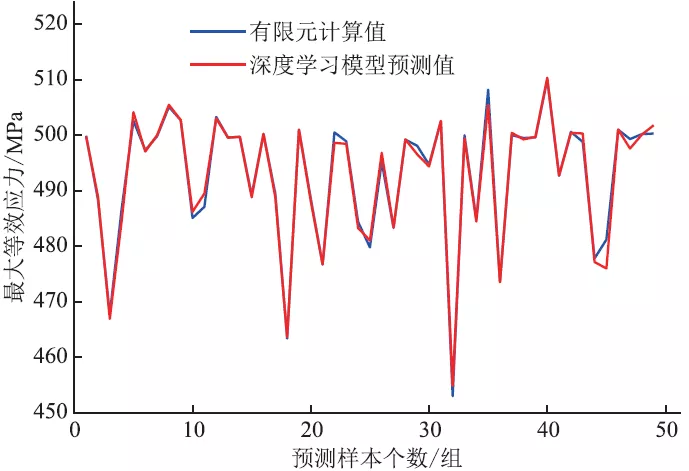
为了验证所训练的神经网络深度学习模型的可靠性，基于有限元方法进行测试集的49 组含不同腐蚀缺陷管道的承载能力分析，并将分析结果与神经网络模型预测结果进行对比（图6）。结果表明：基于深度学习模型预测的含腐蚀缺陷海底管道最大等效应力与基于非线性有限元计算结果基本吻合，相对误差仅为0.003 9，验证了BP 神经网络模型的可靠性，可用于对含腐蚀缺陷海底管道剩余强度的评估。

图6　含腐蚀缺陷管道最大等效应力有限元计算值与深度学习模型预测值对比图

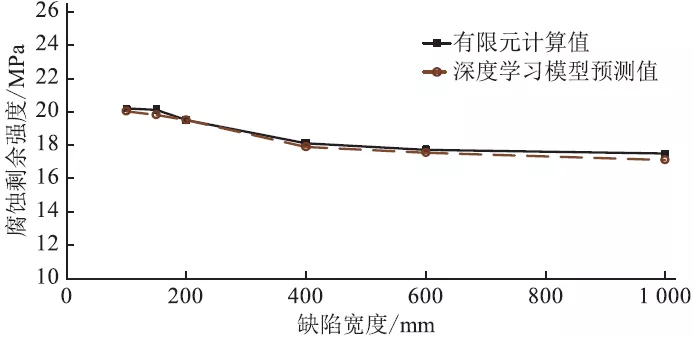
基于所训练的深度学习模型对含腐蚀缺陷管道的剩余强度进行分析，并与49 组测试集的有限元计算结果进行对比，研究了海底管道腐蚀剩余强度与缺陷深度、长度及宽度的关系（图7）。海底管道的腐蚀剩余强度随缺陷深度、长度及宽度的增大均呈下降趋势，但其影响程度各不相同。缺陷深度对管道腐蚀剩余强度的影响显著（图7a），随缺陷深度的增加，管道腐蚀剩余强度逐渐降低，与腐蚀缺陷深度近似线性变化。缺陷长度对管道腐蚀剩余强度的影响明显（图7b），当腐蚀缺陷长度较小（即对于轴向短缺陷）时，随腐蚀长度的增加，管道腐蚀剩余强度降低较快，呈非线性变化；当腐蚀缺陷长度较大（即对于轴向长缺陷）时，随腐蚀长度的增加，管道腐蚀剩余强度降低趋于平缓，缺陷长度的增加对腐蚀剩余强度的影响不大。缺陷宽度对管道腐蚀剩余强度的影响较小（图7c）。

（a）缺陷深度

（b）缺陷长度

（c）缺陷宽度

图7　不同缺陷深度、长度、宽度下管道腐蚀剩余强度有限元计算值与深度学习模型预测值对比图

4　结论

（1）含腐蚀缺陷海底管道的剩余强度与腐蚀缺陷长度、深度及宽度密切相关，腐蚀缺陷的尺寸越大，管道的腐蚀剩余强度越小。缺陷深度对管道腐蚀剩余强度的影响最为显著，缺陷长度次之，缺陷宽度对管道腐蚀剩余强度的影响较小。对于轴向短缺陷，随着腐蚀缺陷长度的增加，腐蚀剩余强度迅速减小；对于轴向长缺陷，腐蚀缺陷长度对腐蚀剩余强度影响较小。

（2）深度学习模型和有限元模型计算得到的管道腐蚀剩余强度评估结果较为接近，吻合度较高。

（3）基于深度学习理论的海底管道腐蚀强度评估模型能够充分考虑含腐蚀缺陷海底管道评估中的非线性因素，且计算速度快、预测精度高，能够用于对含腐蚀缺陷海底管道的剩余强度评估。

免责声明：本网站所转载的文字、图片与视频资料版权归原创作者所有，如果涉及侵权，请第一时间联系本网删除。