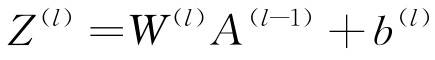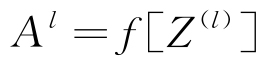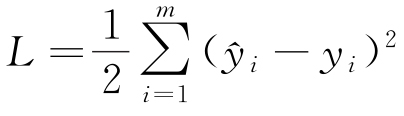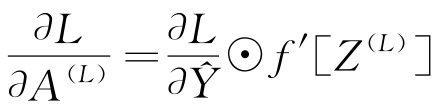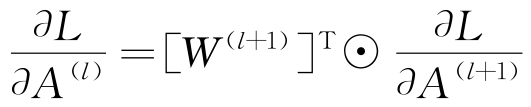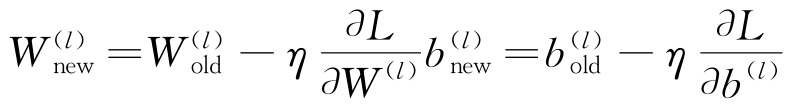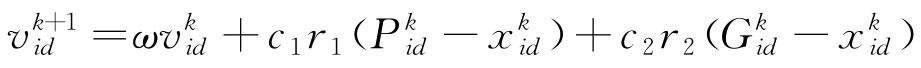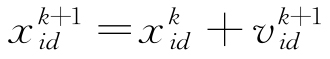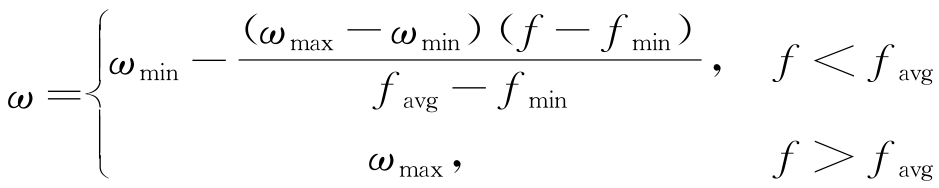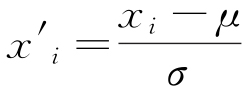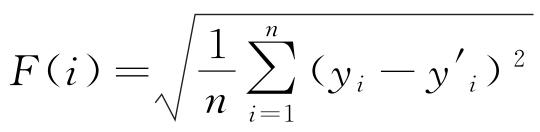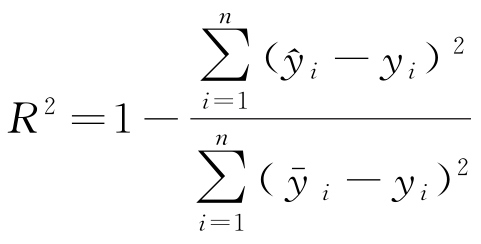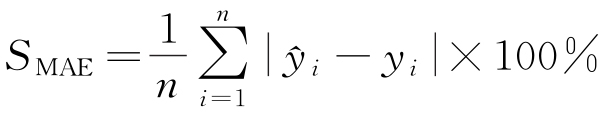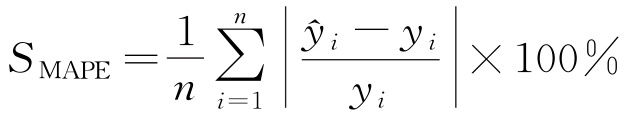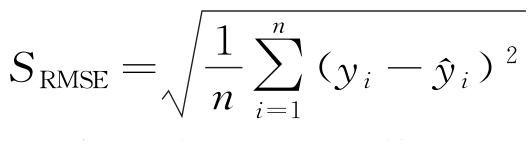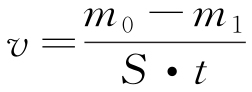APSO-BPNN模型在滨海环境中铁质材料腐蚀速率预测中的应用

2025-01-15 14:43:43 作者：杨彪, 肖佳, 欧阳晨, 朱金晨, 闫莹来源：腐蚀与防护分享至：

铁质材料因其固有的化学活泼性,极易发生腐蚀,尤其是在复杂的滨海环境中,受温度、湿度、盐度、污染物如SO2等多种因素及其耦合作用,其腐蚀问题尤为突出。腐蚀速率作为评估铁质材料在该环境中耐久性的核心指标,其精确预测对于设计有效的防腐蚀措施和延长材料使用寿命具有不可估量的价值。因此,开展滨海环境中的铁质材料腐蚀速率预测研究,成为提升铁质材料防腐蚀性能和保障海洋工程安全的一项重要任务。

由于腐蚀环境的复杂性和非线性特征,传统预测模型难以全面捕捉并准确预测金属腐蚀速率。近年来,机器学习技术凭借其强大的数据处理和模式识别能力,在构建腐蚀预测模型方面展现出了巨大潜力。YAN等[1]提出了一种基于机器学习技术的方法,模拟了低合金钢在海洋大气中的腐蚀行为,评估了材料、环境因素与腐蚀速率之间的关系。姜海生等[2]采用循环神经网络（RNN）对腐蚀探针的监测数据进行训练,建立了管道腐蚀速率预测模型。李昊燃等[3]构建了无偏灰色模型,并通过背景值优化和数据实时更新,引入马尔科夫模型修正预测结果,应用于油气集输管道腐蚀预测,显著提升了预测精度。骆正山等[4]对传统灰色马尔科夫预测模型进行了优化,通过二次平滑处理和白化系数寻优,提高了埋地管道腐蚀速率预测的准确性。前述模型普遍存在对复杂环境适应性不足、参数调优困难等问题。因此,有研究引入了粒子群优化（PSO）算法,通过智能优化模型参数,提升腐蚀速率预测的准确性和稳定性。例如,印翔等[5]提出了基于PSO算法的灰色预测模型,并应用于海底管道腐蚀速率预测。蔡起衡等[6]利用PSO算法优化结合多种机器学习算法构建了Hybrid模型,然后建立了PSO-Hybrid模型,使得平均准确度和马修斯相关系数分别提高了3.3%和8.3%。

现有研究为探明环境因素与铁质材料腐蚀速率之间的关系提供了宝贵的参考。然而,在滨海环境中需要综合考量温度、湿度、氯化钠颗粒物、其他种类污染物及其动态变化等多重复杂因素。这些因素相互作用,形成了一个高度非线性且多维度的腐蚀系统,使得腐蚀速率的预测变得尤为复杂。基于此,笔者利用自适应粒子群优化（APSO）算法对反向传播神经网络（BPNN）中的权重和阈值进行参数寻优,构建了一个APSO-BPNN模型,用于模拟滨海环境中铁质材料的腐蚀速率预测。BPNN因其结构简洁、参数灵活、训练方法多样和易于操作等特点,在众多领域广泛应用[7]。与传统的预测方法相比,BPNN的优势主要体现在其对非线性问题的建模具有更好的适应性和泛化能力。但是,传统BPNN模型对初始权重和阈值的选择高度敏感,训练速率较慢,且容易陷入局部最优解,导致模型泛化能力受限。APSO作为一种启发式全局优化算法,能够通过动态调整粒子群的搜索策略来避免陷入局部最优解,增强了算法的全局搜索能力。APSO结合BPNN的非线性映射能力,不仅能够提高神经网络权重和结构的优化质量,还能够提升模型对复杂滨海环境因素影响下腐蚀速率预测的精确度和鲁棒性。

1. APSO-BPNN理论基础

1.1 反向传播神经网络

BPNN是Rumelhart等[8]于1986年开发的一种标准的多层前馈神经网络,其拓扑结构由输入层、隐藏层和输出层构成,且层间神经元全连接,层内神经元不相连[9]。该网络通过随机初始化连接权重和阈值,并依据训练样本调整这些参数,从而精确映射输入与输出的关系[10]。

算法具体流程如下[11]。

（1）初始化网络参数

权重矩阵W（l）和偏置向量b（l）被随机初始化,l表示层的索引。

（2）前向传播

对于输入层,直接将输入数据X传递到下一层。

对于每一层l,计算加权和Z（l）,见式（1）。

(1)

应用激活函数f来获取激活值Al,见式（2）。

(2)

（3）输出层计算

最后一层的激活值Al作为网络的预测输出。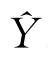

（4）损失函数计算

使用损失函数L来计算预测输出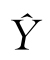和实际输出Y之间的差异,例如均方误差（MSE）,见式（3）。

(3)

式中：m是输出的维度。

（5）反向传播

计算输出层的误差梯度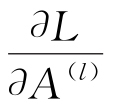,见式（4）。

(4)

对于隐藏层l<L,计算误差梯度,见式（5）。

(5)

（6）权重和偏置更新

计算权重和偏置的梯度,并使用梯度下降法更新,见式（6）。

(6)

式中：η是学习率。

（7）迭代训练

重复步骤（2）至（6）,直到满足某个停止条件,如损失函数值减小到一个可接受的阈值或达到预设的迭代次数。

BPNN的学习过程实际上是信号正向传输和误差反向传播的往复循环过程,通过调整和校正连接权重和阈值来减小输出之间的误差,以达到收敛状态。BPNN在非线性系统的仿真中具有良好的适用性,也适用于大量信息的并行处理[12]。然而,BPNN有一些固有的缺点,包括性能高度依赖于拓扑结构、初始连接权重和连接节点的阈值,并且在训练过程中表现出较慢的收敛速率和较大的波动性,容易陷入局部最优解。因此,为了避免其陷入局部最优,采用一种群体智能学习算法对BPNN进行了参数的寻优改进。

1.2 自适应粒子群优化算法

PSO是一种经典的群智能优化算法,由EBERHART和KENNEDY[13]于1995年提出。它通过使用一种简单的机制来模仿鸟类觅食中的群体行为来引导粒子在搜索空间中运动,从而寻找全局最优值[14]。PSO因其适用范围广、原理简单、超参数少、收敛快、具有较好的全局寻优能力等特点[15-16],而广泛应用于各个领域。

PSO的数学模型定义如下：设有N个粒子组成的种群,表示为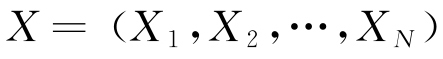,各粒子的位置与速度均为D维向量,其中第i个粒子的位置及飞行速度分别为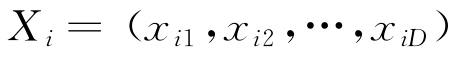和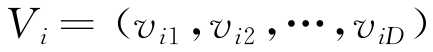,。在算法的迭代过程中,每个粒子的速度和位置表示见式（7）~（8）。

(7)

(8)

式中：k为当前迭代次数；d=1, 2,…,D;ω为惯性权重,用于调节PSO的寻优能力,较大的ω值有利于全局搜索,而较小的ω值则更利于局部优化[17],通常ω∈[0,1]；c1,c2为加速度常数,分别调节粒子向局部最优位置和全局最优位置的迈进步长,通常c1=c2∈[0,2]；r1,r2为相互独立的随机数,均匀分布在[0,1]区间内,用于搜索随机性的增加。粒子在每次迭代中通过追踪个体最优位置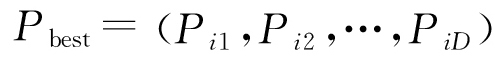和群体最优位置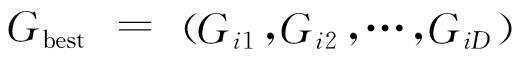,不断更新自身的位置和速度,实现最优解的搜寻[18]。

传统PSO的性能依赖于其参数的选取,其中惯性权重ω是关键参数[19],它决定粒子保持历史速度的程度[20],从而影响算法性能。然而,由于ω的线性递减和信息利用不全,搜索方向缺少指导,且在接近全局最优解时容易产生振荡,这可能导致低收敛速率、局部最优陷阱和过早收敛[21]。为解决这些问题,APSO引入了基于粒子适应度和群体平均适应度的动态惯性权重调整,同时动态改变粒子的飞行时间[22]。

APSO的自适应惯量权重表示见式（9）。

(9)

式中：f为当前粒子的函数值；favg为目标函数的平均值；fmin为全局最优值（最小值）。本文选取ωmax=1.2,ωmin=0.4。

2. APSO-BPNN模型构建

2.1 建模流程

APSO-BPNN模型使用测试集样本进行评估,具体的建模步骤如下,流程示意详见图1。

图 1 APSO-BPNN预测模型流程示意

Figure 1. Schematic diagram of flow chart of APSO-BPNN prediction model

（1）建立BPNN模型

选择隐藏层节点数为7的三层网络结构,训练步长设为100,学习速率设为0.01,目标误差设为0.000 1,使用trainlm函数作为训练函数。激活函数方面,输入层到隐藏层使用logsig函数,而隐藏层到输出层则采用purelin函数。

（2）数据预处理

对采集到的数据（温度、相对湿度以及SO2、NO2、O3、甲酸和NaCl颗粒物的浓度）进行Z-score归一化处理,见式（10）。

(10)

式中：xi为原始数据；σ为样本数据的标准差；μ为样本数据的均值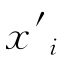；为归一化处理后的数据。

（3）APSO算法参数设置

设置种群规模为30,进化次数定为300。粒子速度的变化范围限定在[-1,1],搜索空间为[-100,100]。惯性权重ω的范围设为[0.4,1.2],加速度常数c1=1.9,c2=1.7。

选择种群规模为30可以在计算成本和搜索多样性之间取得平衡,避免陷入局部最优。进化次数设为300次,保证了充分的迭代次数以实现良好的收敛性。粒子速度范围限定在[-1,1],通过控制步长精确定位最优解。搜索空间设为[-100,100],确保涵盖所有潜在的解区域。惯性权重范围[0.4,1.2]实现了全局探索与局部开发的平衡。加速常数设置为c1=1.9和c2=1.7,在个体和群体影响力之间保持合理的比例,使粒子既能充分探索搜索空间,又能有效收敛到最优解。

（4）适应度函数定义

定义适应度函数F（i）为均方根误差（RMSE）,用于衡量模型预测结果与实际值之间的偏差,见式（11）。

(11)

式中：yi为真实值；为模型预测的输出值；为输出节点的数量。

（5）模型优化

使用APSO算法迭代更新粒子的速度和位置,从而优化BPNN的权重和阈值。优化过程遵循以下步骤：①更新粒子速度和位置；②计算适应度函数值；③更新粒子个体最优位置和全局最优位置；④调整惯性权重以平衡全局搜索和局部搜索。

2.2 模型评价指标

为验证APSO-BPNN模型的有效性,选用以下评价指标来评估模型的预测性能：决定系数（R2）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和均方根误差（RMSE）,具体的计算公式见式（12）~（15）。

(12)

(13)

(14)

(15)

式中：n为测试集样本量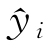；为模型预测值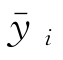；为真实值的平均值；SMAE为平均绝对误差；SMAPE为平均绝对百分比误差；SRMSE为均方根误差。

3. 结果与讨论

3.1 暴露试验结果

滨海区域以其独特的地理位置,常伴随着复杂多变的气候条件及高浓度的海洋性污染物。针对滨海环境特点选取了温度、相对湿度、NaCl质量浓度、SO2质量浓度、NO2质量浓度、O3质量浓度以及甲酸质量浓度七个核心环境因素,以灰口铸铁作为试验材料。经过打磨、清洗、干燥和称量处理后,将试样置于不同环境条件下暴露1 a。根据国家标准GB/T 16545-2015《金属和合金的腐蚀腐蚀试样上腐蚀产物的清除》,对暴露后的试样表面进行化学和物理清洗,以彻底去除腐蚀产物,然后进行干燥和称量。

采用失重法计算试样的腐蚀速率,具体的计算公式见式（16）

(16)

式中：m0为试样暴露前的质量,g；m1为去除腐蚀产物后试样的质量,g；S为试样暴露面积,m2；t为试样暴露时间,a；v为试样的平均腐蚀速率,g/（m2·a）。表1列出了试样暴露的环境因素参数和腐蚀速率。

表 1 试样暴露的环境因素参数和腐蚀速率

Table 1. Exposure environment factor parameters and corrosion rates of samples

试样编号	ρ（NaCl）/（μg·cm-2）	T/℃	相对湿度RH/%	ρ（SO2）/（μg·L-1）	ρ（NO2）/（μg·L-1）	ρ（O3）/（μg·L-1）	ρ（HCOOH）/（μg·L-1）	v/（g·m-2·a-1）
1	5	20	40	1	5	1	10	13.2
2	10	20	40	5	10	25	50	13.0
3	1	20	60	10	20	5	50	8.6
4	30	20	60	20	30	10	10	42.0
5	30	20	70	5	20	1	300	58.0
6	5	20	90	10	10	10	300	32.0
7	10	20	90	20	5	5	100	65.5
8	5	25	40	10	20	25	100	4.0
9	10	25	40	20	30	1	300	9.0
10	1	25	60	1	5	10	300	8.0
11	30	25	60	5	10	5	100	56.0
12	1	25	70	10	10	1	10	26.5
13	5	25	90	1	30	5	50	36.0
14	10	25	90	5	20	10	10	36.0
15	30	30	40	10	5	5	300	13.0
16	1	30	40	20	10	10	100	8.0
17	10	30	60	1	20	1	100	30.2
18	5	30	60	5	30	25	300	7.0
19	10	30	70	10	30	10	50	38.0
20	5	30	70	20	20	5	10	24.0
21	30	30	90	1	10	25	10	105.0
22	1	30	90	5	5	1	50	52.3
23	30	35	40	1	20	10	50	16.0
24	1	35	40	5	30	5	10	8.0
25	10	35	60	10	5	25	10	15.0
26	5	35	60	20	10	1	50	16.0
27	10	35	70	1	10	5	300	25.0
28	5	35	70	5	5	10	100	19.6
29	30	35	90	10	30	1	100	109.0
30	1	35	90	20	20	25	300	11.0

3.2 APSO-BPNN模型效果评估

选取温度、相对湿度RH、NaCl质量浓度、SO2质量浓度、NO2质量浓度、HCOOH质量浓度、O3质量浓度作为模型的输入神经元,试验腐蚀速率作为输出神经元。

（1）传统BPNN模型

为了深入探究优化模型的效果,本文构建并训练了一个传统的BPNN模型,其参数配置与优化后的APSO-BPNN模型保持一致。BPNN模型的训练与预测效果见图2,其中测试集的决定系数R2达到0.801 7,表现出良好的相关性。然而,在评价指标方面,MAE为16.39, MAPE为36.01%, RMSE为20.41,表明模型稳定性有待提高。在对测试集进行预测时,最高相对误差接近60%,这进一步表明该模型对于滨海复杂环境中铁质材料的腐蚀速率预测具有较高的不稳定性。鉴于此,引入APSO算法对BPNN模型的参数进行精细化调整,以提升模型的预测精度。

图 2 传统BPNN模型对滨海环境中铁质材料腐蚀速率的预测结果

Figure 2. Prediction results of corrosion rates of iron materials in coastal environment by traditional BPNN model: (a) training set results and errors; (b) test set results and errors; (c) training set prediction fitting results; (d) test set prediction fitting results

（2）APSO-BPNN模型

如图3所示,随着迭代次数的不断增加,APSO-BPNN模型的适应度呈现出逐步下降的趋势,这得益于APSO算法在迭代过程中多次成功跳出局部最优解的机制,从而确保了全局搜索的有效性。在迭代次数达到236次时,模型成功获得了全局最优解,此时适应度达到了最小值0.005 6。在满足粒子群迭代终止条件后,APSO搜索确定了最终的惯性权重ω为0.719 5。

图 3 APSO-BPNN预测模型适应度曲线

Figure 3. Fitness curve of APSO-BPNN prediction model

将经过APSO算法优化得到的最优权重和阈值引入BPNN模型后,APSO-BPNN模型的训练效果如图4（a）所示,模型训练得到的预测值与真实值高度重合,这充分说明模型训练的高拟合程度。进一步观察图4（a）可以发现,训练集样本的预测值与实际值之间的相对误差均保持在25%以内,且误差波动较小,这充分说明了该模型在训练集上的预测精度较高。如图4（c）所示,训练集决定系数R2高达0.991 3,这进一步印证了预测结果的精确性。

图 4 APSO-BPNN模型对腐蚀速率的预测结果

Figure 4. Prediction results of corrosion rates by APSO-BPNN model: (a) training set results and errors; (b) test set results and errors; (c) training set prediction fitting results; (d) test set prediction fitting results

为了验证经训练集训练的APSO-BPNN模型的精确度,将测试集数据作为输入神经元进行预测,结果如图4（b）所示。可见,APSO-BPNN模型对测试集样本的预测值与真实值之间的相对误差保持在40%以内,且最小相对误差仅为6.9%,误差波动范围较小。在评价指标方面,MAE为11.55, MAPE为22.26%, RMSE为14.43,这表明经过训练集训练的APSO-BPNN模型对未知样本腐蚀速率的预测效果较好,相较于传统BPNN模型展现出较强的泛化能力。如图4（d）所示,决定系数R2达到0.925 8,这进一步证实了在训练小样本数据的情况下,APSO-BPNN模型仍具有一定的预测精度和良好的预测准确性。

综上所述,相较于传统BPNN模型,APSO-BPNN模型展现出了更佳的泛化能力与预测精度,且稳定性更高。在应对较小数据量的腐蚀预测任务时,该模型的预测精度较高,这对于铁质材料的腐蚀速率预测具有重要的实践意义。

4. 结论

为深入探究滨海环境中铁质材料的腐蚀行为,本文选取了温度T、相对湿度RH、NaCl质量浓度、SO2质量浓度、NO2质量浓度、甲酸质量浓度以及O3质量浓度等环境因素,对滨海环境铁质材料腐蚀的行为进行研究。采用失重法计算了铁质材料在多因素环境中暴露1 a的腐蚀速率,并应用机器学习技术对暴露数据进行建模,构建了腐蚀速率预测模型。

对于铁质材料在多因素环境中暴露1 a的腐蚀速率预测,传统BPNN模型的预测效果稳定性不足,其最高相对误差接近60%,决定系数R2仅为0.801 7,预测精度较弱。相比之下,APSO-BPNN模型展现出更佳的泛化能力与预测精度。在迭代寻优过程中,该模型成功多次跳出局部最优,最终在进化代数达到236次时稳定收敛,并确定了最终的惯性权重ω为0.719 5。训练集的决定系数R2高达0.925 8,且相对误差严格控制在25%以内；测试集的决定系数R2同样维持在0.925 8的高水平,相对误差不超过40%。

免责声明：本网站所转载的文字、图片与视频资料版权归原创作者所有，如果涉及侵权，请第一时间联系本网删除。