摘要： 针对镁合金汽车轮毂在实际应用中出现的电偶腐蚀这一难题，建立了轮毂、螺栓连接电偶腐蚀的物理模型和数学模型，推导出电偶腐蚀分析的控制方程式，利用有限元方法结合移动网格技术，模拟研究了镁合金轮毂-钢质螺栓连接在NaCI溶液中的电偶腐蚀行为，得到了连接螺栓沉孔深度和沉孔半径对轮毂腐蚀深度的影响规律；并通过轮毂-螺栓连接偶对金属的全浸试验，验证了镁合金轮毂-钢质螺栓连接电偶腐蚀模拟分析方法的正确性。结果表明:随着沉孔深度增加，平均腐蚀深度先增加后减小；随着沉孔半径增加，平均腐蚀深度逐渐减小，而连接边缘处最大腐蚀深度先增加后近似保持不变。

关键词： 镁合金轮毂；螺栓；电偶腐蚀；数值模拟；腐蚀深度

1　镁合金轮毂-螺栓连接电偶腐蚀仿真模型

1.1　物理模型

图1为镁合金轮毂-螺栓连接的三维简化模型示意图。由图1可见:当轮毂的螺栓沉孔中积存电解质时，由于镁合金和钢质紧固螺栓直接接触，而且通过电解质环境构成回路，会形成腐蚀原电池，造成镁合金轮毂腐蚀加速。

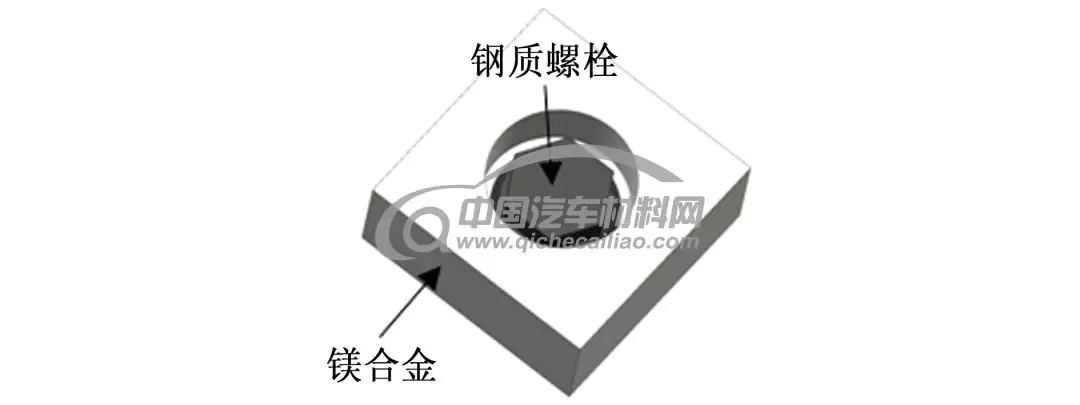
图1　轮毂-螺栓连接的模型

选用3.5%(质量分数，下同)NaCl溶液作为电解质溶液，为了进一步简化模拟，采用理想的二维轴对称模型代替三维模型，简化方法如图2所示，选取abcd区域为研究对象，阴极边界简化为螺栓头部在垂直方向的投影线段，dc段长度为螺栓沉孔深度H，bc段长度为螺栓沉孔半径R。二维轴对称模型网格划分图如图3所示，对电解质区域进行网格划分，由于阳极腐蚀时发生电化学溶解，为了准确模拟阳极腐蚀深度，在边界处采用较密的网格划分。

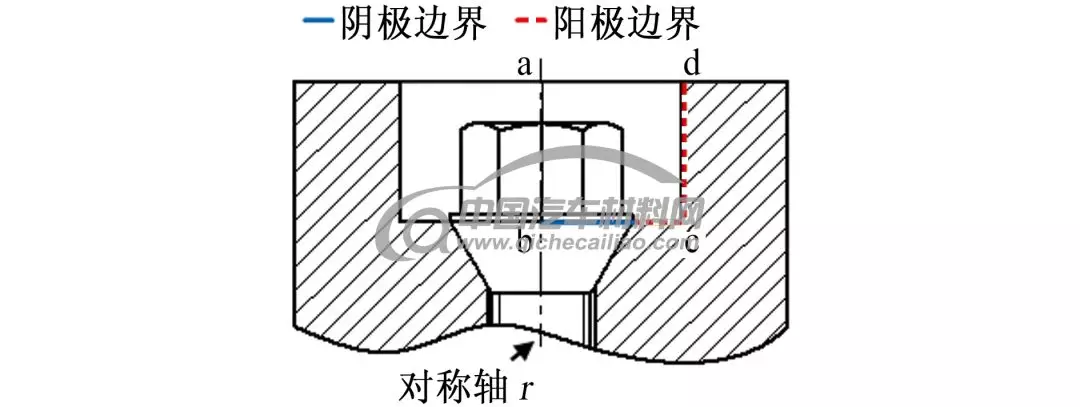
图2　三维模型简化方法示意图

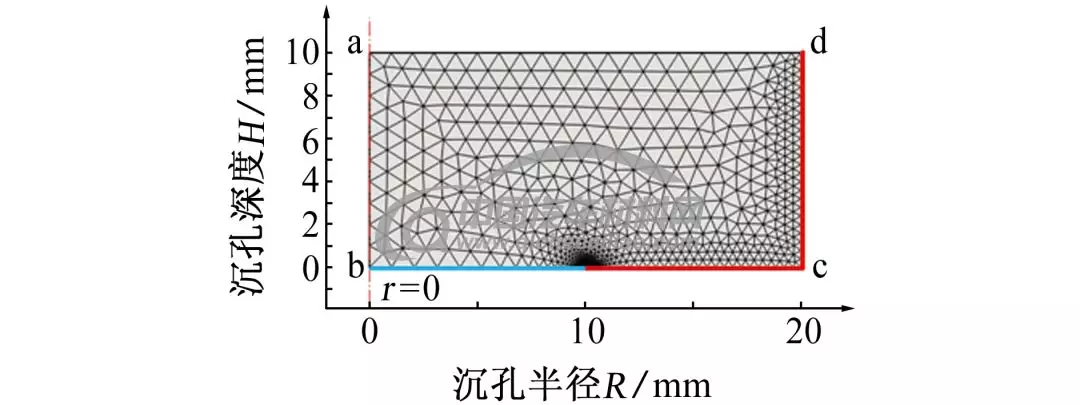
图3　二维轴对称模型网格划分图

1.2　数学模型

为了使所建立的模型能够准确模拟腐蚀行为以及研究主要几何因素对电偶腐蚀的影响,在DESHPANDE[11]的研究基础上建立数学模型，模拟AE44镁合金轮毂与MS钢质紧固螺栓连接在3.5% NaCl溶液中的电偶腐蚀行为。

1.2.1 控制方程

本模型电解液中物质i的传递可用Nernst-Plank方程描述:

1.2.2 边界条件

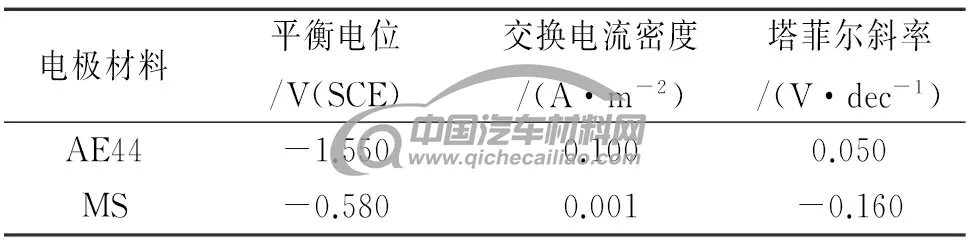
求解电偶腐蚀过程模型时，电极表面的边界条件为求解腐蚀速率的关键，要求通过数值方法描述电极材料工作时电流密度与电位之间的极化关系作为电极表面的边界条件。采用Tafel方程描述这一关系，AE44镁合金和MS低碳钢的极化曲线参考DESHPANDE[12]的测量结果，极化动力学参数列于表1。

表1　Tafel曲线的拟合参数

Tab. 1　Fitting parameters of Tafel curves

阳极表面的边界条件为

2　仿真结果与讨论

利用二维轴对称模型模拟研究室温下AE44镁合金-MS低碳钢电偶对在3.5% NaCl溶液中浸泡72 h，镁合金表面腐蚀深度随时间的变化如图4所示。其中，阴极边界宽度为10 mm，沉孔半径(R)为20 mm，螺栓沉孔深度(H)为5 mm。

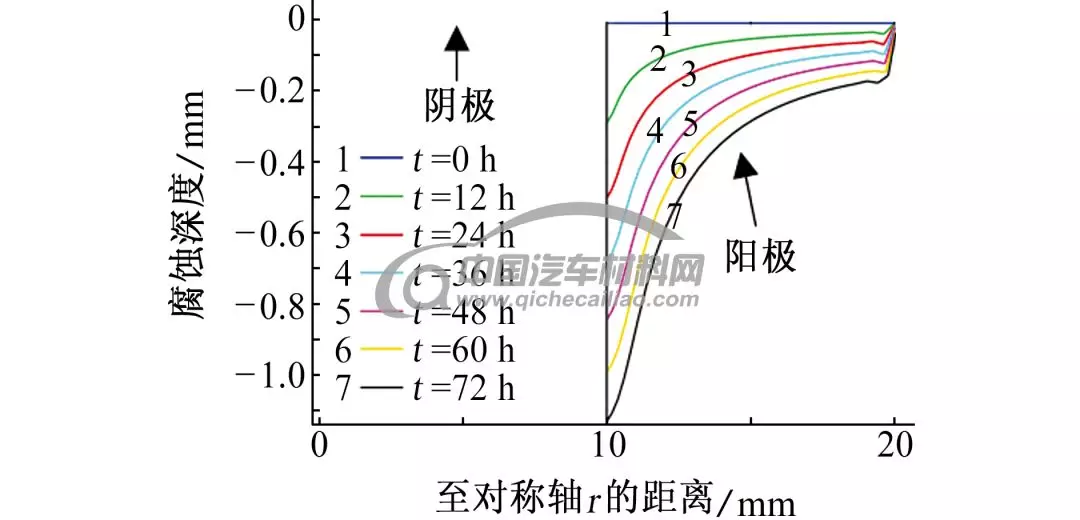
图4　电偶对在3.5% NaCl溶液中浸泡不同时间后，镁合金腐蚀深度随时间的变化曲线

浸泡72 h后，镁合金表面距偶接位置越近，蚀坑越深，在阴阳极接触区域附近出现一圈很深的腐蚀坑，蚀坑深度大于1 mm，随着与接触位置距离增加，腐蚀速率变缓。在电偶腐蚀初期，腐蚀会迅速沿横向扩散，随着电偶腐蚀的进行，腐蚀主要沿垂直方向扩展，形成腐蚀坑。

2.1　螺栓沉孔深度对电偶腐蚀的影响

螺栓沉孔半径为20 mm，改变螺栓孔深度，室温下螺栓沉孔内充满3.5% NaCl溶液，浸泡偶对金属72 h后，考察镁合金的腐蚀深度分布情况。若不考虑沉孔侧壁的腐蚀，即假设模型中cd段绝缘，如图5所示：随着H的增加，在阴阳极接触位置的最大腐蚀深度由1.32 mm减小到1.17 mm，但与接触点距离超过1.5 mm后，腐蚀深度随H的增大而增大。这主要是由于当H减小时，沉孔内电解质溶液的厚度减小，溶液电阻增大，抑制电流流到远离接触位置的区域[13]，从而造成电偶电流的分布不均匀，在远离阴阳极金属接触位置的阳极金属腐蚀深度随之减小；另外，电解质溶液厚度越小，阴阳极金属接触位置附近溶液中的电位梯度增大，则带电离子运动的速率增加，电化学反应速率增加，造成接触位置附近的阳极金属腐蚀深度随之增大。当H增大，电偶电流的分布范围变广，腐蚀变得均匀。不同H时镁合金表面电偶电流密度的分布如图6所示。

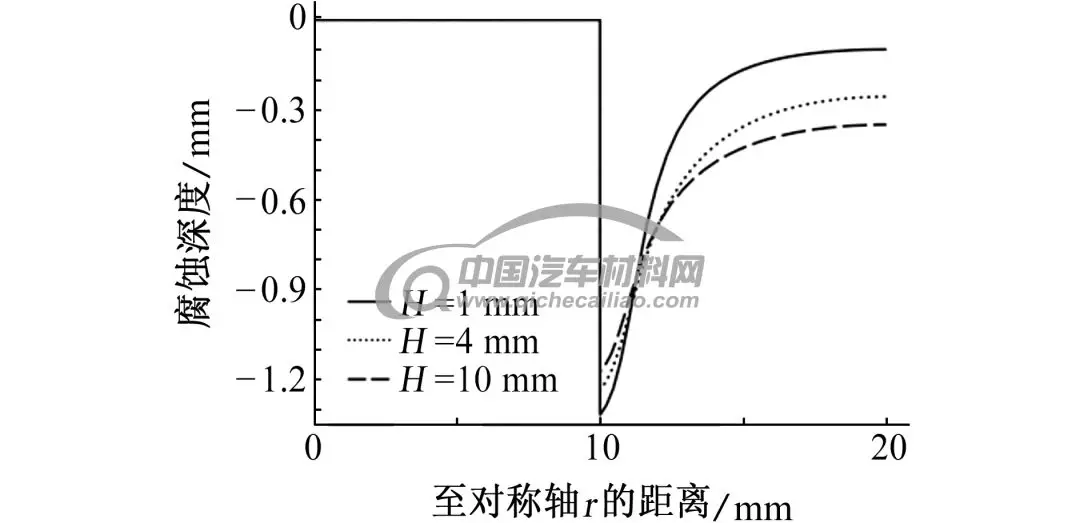
图5　不同H电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金腐蚀深度随时间的变化曲线

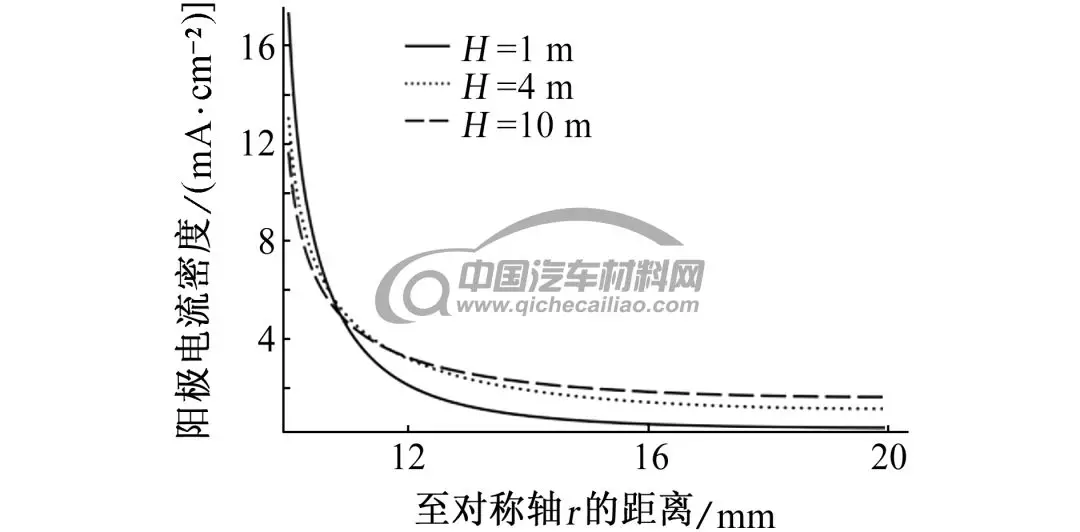
图6　不同H电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金阳极电流密度随时间的变化曲线

不考虑沉孔侧壁的腐蚀，镁合金平均腐蚀深度随H的变化如图7(a)所示，H小于10 mm时，随着沉孔深度增加，沉孔内电解质厚度增加，平均腐蚀深度增加；H大于10 mm时，平均腐蚀深度变化不显著。实际环境中，沉孔的侧壁作为阳极金属参与电偶腐蚀，将模型中的cd段设置为参与电偶腐蚀过程的阳极金属，随着H增加，电偶腐蚀的阴阳极面积比减小，电偶腐蚀程度会有所减弱。在电解质溶液厚度和阴阳极面积比的共同影响下，镁合金平均腐蚀深度随H的变化规律如图7(b)所示，H小于5 mm，H变化引起的电解质溶液厚度的变化是影响腐蚀平均深度的主要因素；H大于5 mm，电解质溶液厚度变化对平均腐蚀深度的影响不再明显，H变化引起的阴阳极面积比变化成为影响平均电偶腐蚀深度的主要因素。

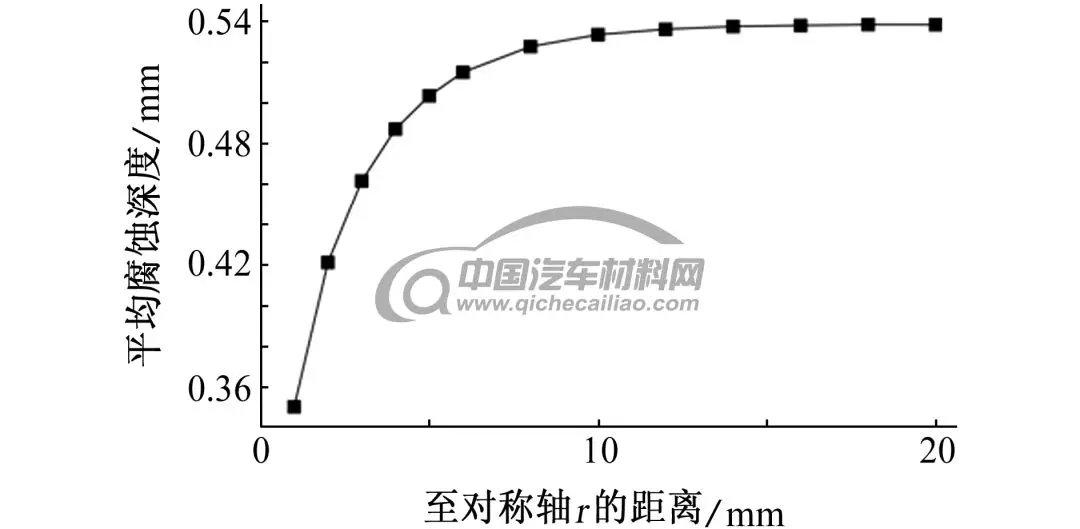
(a)　不考虑侧壁腐蚀

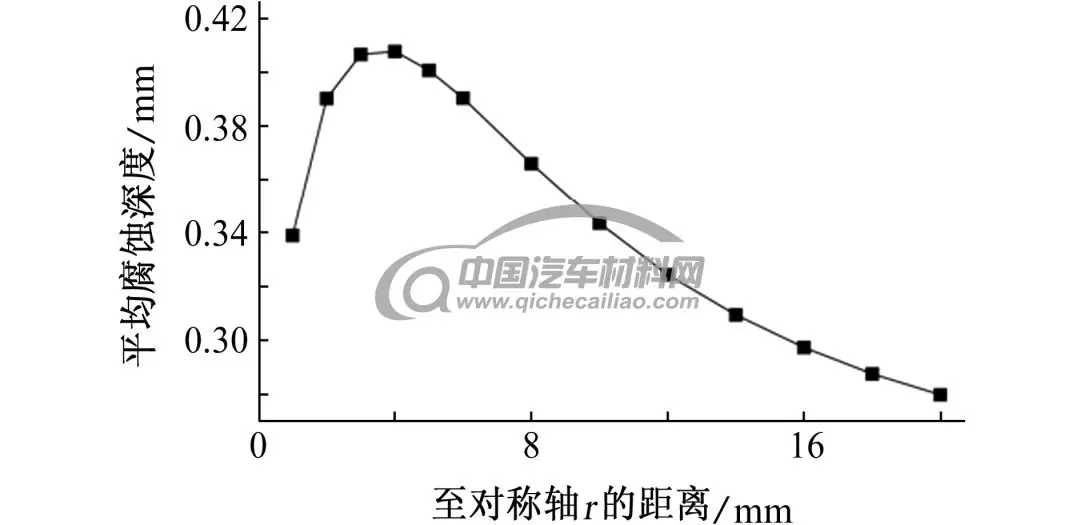
(b)　考虑侧壁腐蚀

图7　不同H电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金腐蚀深度

2.2　螺栓沉孔半径对电偶腐蚀的影响

实际使用环境中，轮毂螺栓沉孔内积存的雨水、泥土等电解质的体积一定，不同沉孔半径(R)会造成积存电解质的厚度发生变化，同时也会改变电偶腐蚀偶对金属的阴阳极面积比，从而影响电偶腐蚀的严重程度。模拟研究室温下螺栓沉孔内积存恒定体积2 000 mm3的3.5% NaCl溶液，浸泡偶对金属72 h后，不同R对镁合金的腐蚀深度分布情况的影响,见图8。

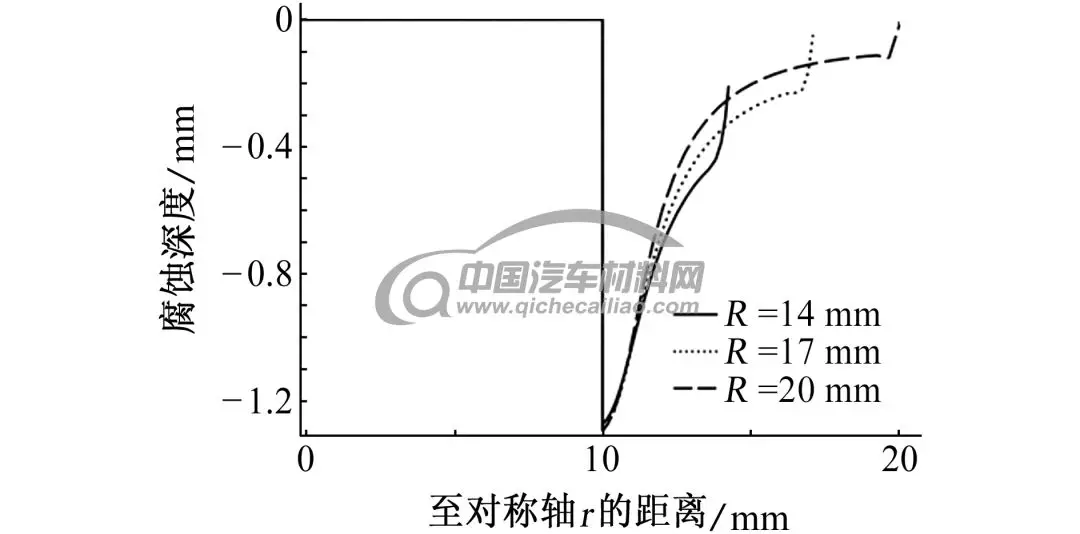
图8　不同R电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金腐蚀深度随时间的变化曲线

由图8可见：R的变化对腐蚀深度的影响主要表现在距离接触点一定距离之后，腐蚀深度随着R的增大而减小。平均腐蚀深度的变化规律如图9所示，图10给出了接触点附近的最大腐蚀深度随着R的变化规律，随着R增大，电解质厚度减小的同时阴阳极面积比减小，镁合金平均腐蚀深度逐渐减小，接触位置附近最大腐蚀深度先明显增加，R大于15 mm后，最大腐蚀深度近似保持不变。

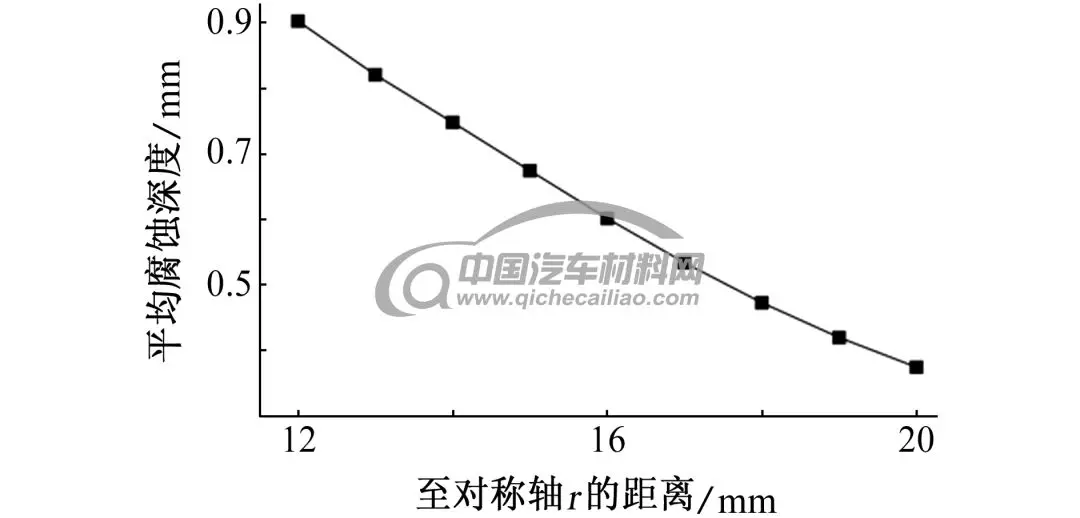
图9　不同R电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金腐蚀深度

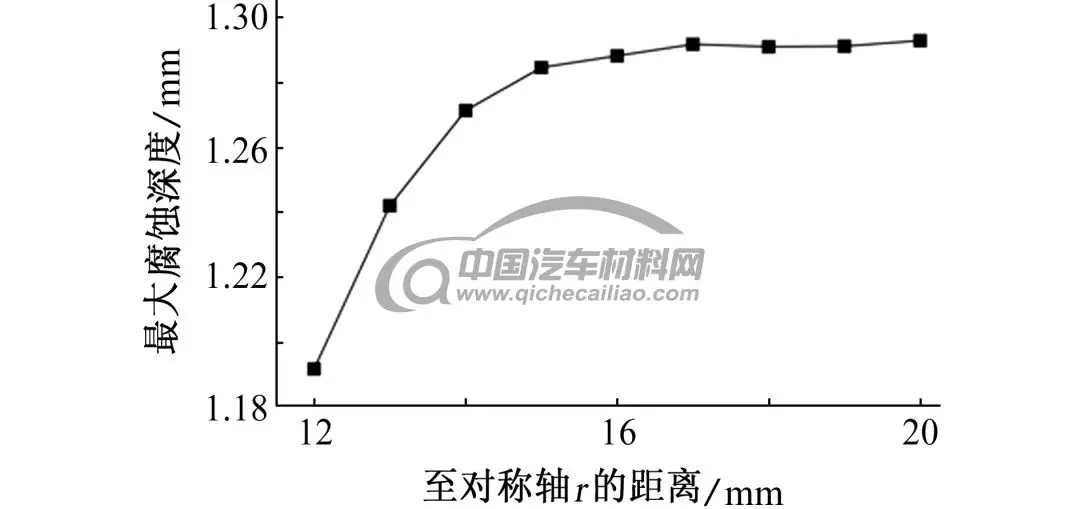
图10　不同R电偶对在3.5% NaCl溶液中浸泡72 h后，镁合金的最大腐蚀深度

3　试验结果与仿真结果的对比

4　结论

(a)　3 h (b)　6 h (c)　12 h (d)　24 h

图11　浸泡试验和仿真试验结果对比

参考文献：

[1]卫英慧，许并社. 镁合金腐蚀防护的理论与实践[M]. 北京:冶金工业出版社，2008.

[2]张新，张奎. 镁合金腐蚀行为及机理研究进展[J]. 腐蚀科学与防护技术，2015(1):78-84.

[3]曾荣昌，陈君，张津. 镁合金电偶腐蚀研究及其进展[J]. 材料导报，2008，22(1):107-109.

[4]CROSS S R,GOLLAPUDI S,SCHUH C A. Validated numerical modeling of galvanic corrosion of zinc and aluminum coatings[J]. Corrosion Science,2014,88(88):226-233.

[5]THAMIDA S K. Modeling and simulation of galvanic corrosion pit as a moving boundary problem[J]. Computational Materials Science,2012,65(3):269-275.

[6]JIA J X,SONG G,ATRENS A. Influence of geometry on galvanic corrosion of AZ91D coupled to steel[J]. Corrosion Science,2006,48(8):2133-2153.

[7]THÉBAULT F,VUILLEMIN B,OLTRA R,et al. Reliability of numerical models for simulating galvanic corrosion processes[J]. Electrochimica Acta,2012,82(21):349-355.

[8]DESHPANDE K B. Effect of aluminium spacer on galvanic corrosion between magnesium and mild steel using numerical model and SVET experiments[J]. Corrosion Science,2012,62(9):184-191.

[9]刘贵昌,孙文,王立达. 海水中牺牲阳极阴极保护的分段非线性边界数学模型[J]. 腐蚀与防护,2012(10):876-879.

[10]　高福勇，赵明，何广平，等. AZ31镁合金微区电偶腐蚀的数值研究[J]. 北京科技大学学报，2013，35(5):634-641.

[11]DESHPANDE K B. Experimental investigation of galvanic corrosion:comparison between SVET and immersion techniques[J]. Corrosion Science,2010,52(9):2819-2826.

[12]DESHPANDE K B. Validated numerical modelling of galvanic corrosion for couples:magnesium alloy (AE44)-mild steel and AE44-aluminium alloy (AA6063) in brine solution[J]. Corrosion Science,2010,52(10):3514-3522.

[13]SONG G,JOHANNESSON B,HAPUGODA S,et al. Galvanic corrosion of magnesium alloy AZ91D in contact with an aluminium alloy,steel and zinc[J]. Corrosion Science,2004,46(4):955-977.