通过设计计算来预测构件或零件的疲劳强度和疲劳寿命，是多少年来无数学者和工程技术人员孜孜以求的目标。但是至今还没能够形成一种对实际工程适用的、比较准确的疲劳强度和寿命的计算方法。这是因为研究对象在结构上的千变万化、加工制造工艺及其质量的不稳定性、材料组织性能不稳定性和内部及表面缺陷的不确定性、外部载荷的复杂和随机性以及结构的动态响应问题等等，诸如这些因素很难归纳成为一个统一的物理或数学模型。因此至今关于疲劳强度的计算都有一定的误差存在甚至误差很大。即使计算结果是比较准确的，其结果也具有统计性，而不是针对每一个零部件而言。

对于新产品的开发，应至少对于某些重要零部件等同时进行试验研究和试验验证。如果受试验条件等的限制，可以根据零部件的特点进行合理简化来进行模拟性试验，这也是非常有用的。诸多纷杂的因素中，对于疲劳强度危害最大的是应力集中。

因此，从设计和制造的过程来看，危害最大的有以下几点：

第一是结构的不合理性；第二是工艺缺陷如焊接缺陷、机械加工缺陷、材料内部缺陷，还包括偶然因素造成的表面伤痕等等；第三是材料的选择。因此如果为提高疲劳强度，在设计和制造过程中最重要的就是降低应力集中。对于实际零部件还需要注意的是，因为其往往带有形状缺口，所以未必选择高强度钢就可提高其疲劳强度。

到目前为止，疲劳强度的设计实质上还是基于大量试验结果的估算。近年来已经出现了有关疲劳强度设计的专用软件，使得这项工作的效率更高和更易趋于合理准确，但对于它的使用同样需要具有一定的疲劳强度设计的经验。

疲劳强度设计包括疲劳安全系数的校核和疲劳寿命的估算两项内容。具体的设计计算方法有应力-寿命法和局部应力-应变法。局部应力应变法目前还只适用于零部件的应力集中处发生了塑性变形的低周疲劳。应力-寿命设计法主要用于只发生弹性变形的高周疲劳，设计所用的基本参数是零部件危险点处的名义应力，所以这种方法又叫名义应力法，它的研究和使用历史较长，资料丰富，至今仍被广泛使用。名义应力法包括无限寿命设计和有限寿命设计两种设计思路，本节只就名义应力法的内容进行讨论。

名义应力法的关键点也是它的难点有三点，一是疲劳极限降低系数和应力-寿命曲线的确定，二是危险点应力的确定计算，三是外载荷的获得。而要解决好这些问题，计算和试验两点都不可忽略。

一、无限寿命设计法

无限寿命设计法的基本思路是，使得零件或构件的危险部位的工作应力低于其疲劳极限，从而保证它在设计的工作应力下能够长久工作而不发生破坏。当零件的结构比较简单应力集中较小时，恒幅交变应力、过载应力小且次数很少时可用这种方法。对应力集中较大的构件使用该方法进行疲劳强度设计将会使结构变的粗大笨重。对于过载应力较大且次数较多的交变载荷情况和随机载荷一般也不宜采用此种方法。

（一）对称循环载荷：

R=-1，疲劳强度条件为

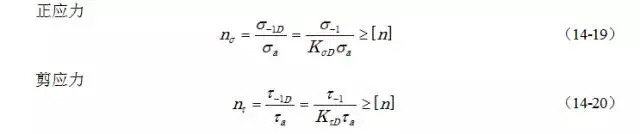
式中：KσD，KτD是对称循环下零件的疲劳强度降低系数，它包含了前面讨论的疲劳强度的诸影响因素。该系数的选择无疑将对疲劳强度的估算产生很大的影响。它有多种计算用经验表达式形式，现只列出比较常见的几种。

式中， Kσ，Kτ：疲劳缺口系数，ε：尺寸系数，β：表面加工系数。

以上三式的主要不同点在于对表面加工系数β的处理。第一式认为β、Kσ、ε三者互不影响；第二式认为β随着Kσ的增加而减弱；第三式认为β随着Kσ/ε值增加而减小。从试用的情况来看，在Kσ较低的范围内三者的差别不大。在Kσ较大的情况下，第一式的结果偏大，而第二式的结果比第三式的结果略大。关于表面粗糙度等表面加工情况对疲劳缺口系数的影响，未见到有关的研究报道。但参照多重缺口材料的疲劳缺口系数的研究结果推断，随着疲劳缺口变尖锐表面粗糙度的影响不应增大。考虑材料强度对表面加工系数的影响，高强度钢适合采用第二式，而对于塑性比较好的低中强度钢适合采用第三式。

（二）不对称循环载荷：

1.R保持不变时的疲劳强度条件为

式中，σaD，τaD：应力比为R时的疲劳极限；σm，τm：平均应力；ψσ，ψτ：平均应力折算系数，对于Goodman方程有ψσ=σm/σb，其他符号意义同上。

式中符号意义同上。

二、有限寿命设计法

当交变载荷有较多的冲击过载或工作载荷为随机载荷时，工作应力在某些时刻会越过疲劳极限。此时，疲劳寿命设计主要是保证构件在设计的寿命之内不发生疲劳破坏而正常工作，也即设计使构件具有有限的疲劳寿命。考虑到偶然因素的影响，为确保安全在设计时一般使设计寿命为使用寿命的数倍。

有限寿命设计法主要基于疲劳累积损伤理论，故先作简单介绍然后讨论疲劳强度校核问题。

（一）迈因纳累积损伤理论

金属疲劳累积损伤的假说多达数十种，但其中最简单、适用的是迈因纳(Palmgren-Miner)理论，习惯称之为线性累积损伤理论。迈因纳理论认为材料的疲劳破坏是由于循环载荷的不断作用而产生损伤并不断积累造成的；疲劳损伤累积达到破坏时吸收的净功W与疲劳载荷的历史无关，并且材料的疲劳损伤程度与应力循环次数成正比。设材料在某级应力下达到破坏时的应力循环次数为N1、经n1次应力循环而疲劳损伤吸收的净功为W1，根据迈因纳理论有

则在i个应力水平级别下分别对应经过ni次应力循环时，材料疲劳累积损伤为

式中，ni：第i级应力水平下经过的应力循环数；Ni：第i级应力水平下的达到破坏时的应力循环数。当D值等于1时，认为被评估对象开始破坏。

应该指出迈因纳理论没有考虑加载顺序的影响和平均应力的影响，只是一种近似理论。但是，由于该理论简单便于利用，在工程上得到了广泛应用。针对线性累积损伤理论所存在的问题，又提出了非线性累积损伤理论以提高其计算精度，但应用不如前者广。

 （二）随机载荷的处理

零部件承受的变幅载荷尤其是对承受随机载荷是需要测得到。利用累积损伤理论进行疲劳设计时，需要先对实测得到的载荷-时间历程进行编谱，即用概率统计的方法将其简化成典型的载荷谱或应力谱。因为引起疲劳的最根本的原因是动载分量应力幅值和它的循环次数，所以一般用统计记数法来处理波形与频次的关系等问题。在各种统计记数法中，被国际上广泛用于疲劳强度设计的是雨流计数法，它被认为最符合材料的疲劳损伤规律。这种方法把整个载荷-时间历程中出现的应力幅范围划分为若干个等差的应力幅级别，然后统计出各级应力幅级别内所出现的循环次数，从而得到载荷-频次曲线等各种形式的载荷的统计结果。

实测的载荷-时间历程的半波数往往是数以几十万、几百万个，用手算的方法几乎是不可能的。所以工程上编制了雨流法的计算机处理程序，可以便捷地进行编谱分析。

（三）疲劳强度校核

设计中为保证不发生疲劳破坏，需D≤1，即

式中，N0：S-N曲线的拐点对应的循环数；σ-1：材料疲劳极限；σi ：第i级应力水平的应力幅；Ni：第i级应力水平的循环应力作用下，材料达到破坏时的应力循环次数；N ：设计疲劳寿命即总应力循环次数；ni：在设计疲劳寿命下第i级应力水平的循环次数；ni/N：第i级应力的循环次数与总应力循环次数之比，当载荷谱已知时为一不变值。

可见随着设计寿命的增加，等效应力增大而安全系数降低。

（四）疲劳寿命估算

根据迈因纳理论，达到疲劳破坏时有

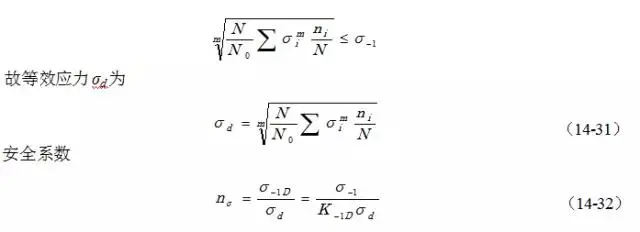
式中：NT为载荷谱下出现损伤的循环次数即所求的总寿命；ni为i级应力水平σi的循环次数；αi为i级应力水平σi的循环次数在总寿命中所占比例；Ni表示在应力σi作用下导致破坏的循环数。在应力谱已知的情况下，Ni的估算是此项估算工作的关键。

对于每级应力水平下导致的破坏循环寿命的确定，可参照工程标准，许多软件安排了一些常用的准则供用户选用。这里仅以I-Deas为例，即：

（1）应力-寿命（Stress life）准则

（2）应变-寿命（Strain life）准则

（3）SWT准则（Smith-Watson-Topper）

（4）美国机械工程学会（ASME）锅炉和压力容器规范

（5）英国焊接研究所（BWI）公式（Btitish Weld Institute formulation）

另外，它还允许用户自定义些特殊的应力或应变寿命准则，程序为此已留有相应的接口。

以应力-寿命（Stress life）准则确定Ni，是依据材料的应力寿命曲线或零件本身的应力寿命曲线的斜线部分来确定。首先可用应变片测定危险点处的应力或用材料力学或有限元等方法求出危险点的应力幅σa，然后再根据斜线部分求出对应于相应应力水平的断裂寿命即为所求Ni。如果使用零件的S-N曲线进行计算则可直接根据此曲线求得对应于应力幅σa的Ni。也可先根据材料的S-N曲线等现有资料对材料的S-N曲线进行修整从而得到画出零件的S-N曲线，然后进行与上相同的Ni的计算。在以上三种方法中，要根据所掌握资料的情况，优先选择最接近所设计对象的一种。

三、复合应力下的疲劳强度设计

以上讨论是单向应力的情况，对于复合应力的情况也也有类似的疲劳强度校核与疲劳寿命的估算方法，只是此时所用的应力幅变成了对应强度理论下的等效应力幅，下面作一简单讨论。

在构件危险点处的应力分别为sx、sy、sz、txy、tyz、tzx时，该处的第三、第四强度理论的等效应力分别为

式中，KsD、s-1、sd为疲劳强度降低系数、材料的疲劳极限和对应的等效应力。

试验表明，在平面弯扭组合疲劳应力s、t的情况下，当材料达到疲劳破坏时满足如下方程

式中，s-1、t-1分别为材料的弯曲和扭转的疲劳极限，此式由高夫首先提出。该式两边同乘以s-1并开方，有

对于s-1、t-1，在第三、第四强度理论时分别有

故上式又可变为

故上式又可变为

式（14-39）式（14-40）正好是式（14-32）和式（14-33）在平面弯扭组合情况下的结果。由零件的疲劳强度校核条件式（14-36）及式（14-38），有

设ns=s-1/s，nt=t-1/s-1，分别为纯弯和纯扭转时安全系数，则上式为

以上疲劳强度校核公式适用于钢等延性材料，载荷为对称循环。

对于非对称循环载荷，有类似公式

式中，srd：应力比为r时的等效应力

式中，ψσ：平均应力折算系数，见式（14-26）。